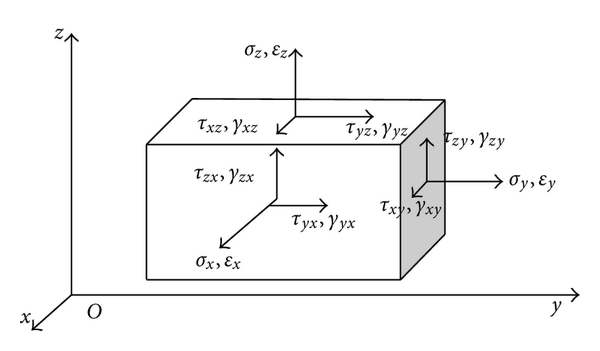
Strain is a measurable effect in an engineered components caused by the application of a force to that component. Although there are several types of strain used in different situations, the most commonly used is the normal strain, which is defined as the deformation per unit length.
Stress and Strain
Stress is proportional to strain by a factor called Young’s Modulus, notated as E. Young’s Modulus is the modulus of elasticity of the material and defines how “stretchy” or “stiff” the material is. This relationship between stress and strain is called Hooke’s Law. Because stress can also be defined as the ratio between the applied load and the cross sectional area, strain can also be defined in terms of these factors.
Normal strain is plotted against stress to obtain stress-strain curves for different materials. Stress-strain curves provide information on the material properties of the component material, including ultimate strength, yield strength, and ductility. Please refer to the figures accompanying this article for an example of a stress-strain diagram and commonly used equations for strain.
Measuring Strain
Because strain is a function of displacement, measuring strain is a function of measuring displacement. For small displacements, strain gauges are most often used. Single strain gauges are most appropriate for uniaxial loading situations. Extensometers are often used for situations where larger displacements are expected, and are also appropriate for uniaxial loading modes. In addition to these methods, optical technologies can be used to measure strain. In this case, a high resolution camera monitors a target on the loaded component. Using this method, strains can be measured in multiple directions.
Engineering Strain vs. True Strain
The strain defined by the change in length dvided by the unit length of a component assumes that the cross sectional area of the component remains constant as the component stretches or is compressed. Technically, this is not true. When a component is loaded axially, it’s cross section actually changes. As the component is stretched under a tensile load, the cross sectional area decreases.
As the component is squashed under a compressive load, the cross sectional area increases. These changes are slight, but can be significant in some cases. The standard strain definition is called “engineering strain”. However, a more accurate version can be computed by examining the incremental changes in a component as it is loaded and it deforms. Please refer to the figures accompanying this article for the equation for true strain.
Strain is a critical value that must be understood in engineered structures to ensure that the structure is adequate for its intended loading environment.